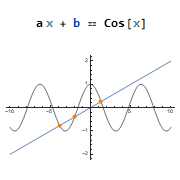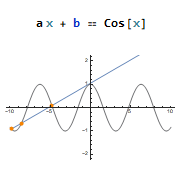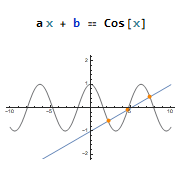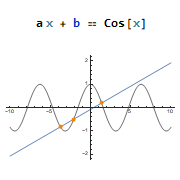Mathematical notation, special-character aliases, entering Greek letters and formulae. Converting expressions to and from LaTeX code.
Everything is an expression: a unified form for operators, functions, objects, and data structures. Expressions Part[] ([[]]), FullForm[], and TreeForm[]. Symbolic computation principles: patterns and replacement rules. Variables and functions as global replacements, expressions Set[] (=) and SetDelayed[] (:=).
Functional programming: anonymous functions (&) and arguments (#, #2, …), prefix (@) and postfix (//) notations, pattern tests and polymorphism, listability. Higher-order functions: Apply[] (@@ and @@@), Map[] (/@), Nest[], NestList[], and Fold[].
Plot[], ListPlot[], ParametricPlot[], and other plotting expressions. Plot options and substitutions. Combining plots with Show[].
Dynamic outputs and interactive expressions, Manipulate[].
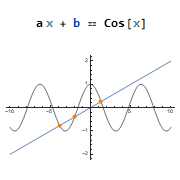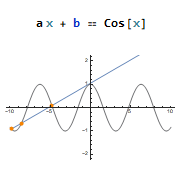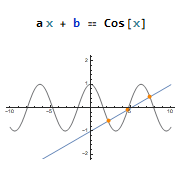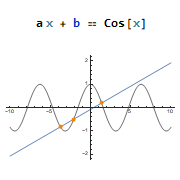
Localized replacement rules: Rule[] (->, →), ReplaceAll[] (/.), and ReplaceRepeated[] (//.). Expression Equal[] (==). Analytical and numerical expressions for solving algebraic equations: Solve[], NSolve[], and FindRoot[], parameters and domain specification. Applying and plotting solution results.
*RuleDelayed[] (:>, :→).
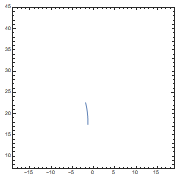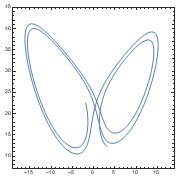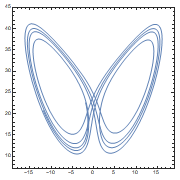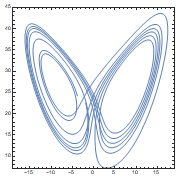
Analytical and numerical differentiation and integration: D[] ('), Integrate[] (∫), and NIntegrate[] expressions. Analytical and numerical expressions for solving Differential Equations (ODE) and Differential-Algebraic systems of Equations (DAE): DSolve[] and NDSolve[], constaints and initial conditions. Plotting the solutions.

Graphics[] expression, graphical primitives, styling options. Adding graphical primitives to Plots, evaluated form of a Plot[], embedding Plots into Graphics[]. Exporting plots and graphics as .pdf files.
Parametric animation and exporting frame sequences.